XGBoost (2)

From last article, I have showed how to decide the value for each tree node in order to obtain the minimum loss. The techniques for solving that problem are Tyler Formula and transformation from sample to node.

But still, that optimal solution is under the assumption that the tree structure is fixed, meaning for each data sample, we know which leave node it belongs to. So the question is: how to split the tree?

1. Tree Splitting Algorithm

1.1 Splitting Gain

To know how to split the tree, first we need to set up a rule to decide the goodness of this split. Remember from last post we get the structure score: \[obj = -\frac{1}{2}\sum_{j=1}^{T}\frac{G^2_j}{H_j+\lambda}+\gamma T\] Which basically tells us under this tree structure, what is the total loss. And if we ignore \(T\) which tells us the depth of the tree, actually this term \(-\frac{G^2_j}{H_j+\lambda}\) describes how the samples in each node contribute to the total loss, the less, the better. (remember \(G_j = \sum_{i\in I_j}g_i\), \(H_j =\sum_{i\in I_j}h_i\)). In turn, \(\frac{G^2_j}{H_j+\lambda}\) describes how the samples in each node contribute to the total gain, the larger, the better.

So by using this information, we can summarize an expression for measuring the gain of the split:

\[Gain = \frac{1}{2}[\frac{G^2_L}{H_L+\lambda}+\frac{G^2_R}{H_R+\lambda} - \frac{(G_L+G_R)^2}{H_L+H_R+\lambda}]-\gamma\] Where \(\frac{G^2_L}{H_L+\lambda}\) tells the gain for the left subtree, \(\frac{G^2_R}{H_R+\lambda}\) tells the gain for the right subtree. And \(\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}\) tells the gain if we don't split tree. And eventually \(\gamma\) is the price for adding a new tree. So to sum them up, The total gain is the combination of left gain plus right gain minus no splitting gain and tree complication penalty.

Normally we will set up a threshold, if the gain smaller the threshold, we will not allow this split.

After knowing how to decide whether this split is good or not by looking at the gain value, then let's look at the algorithm we will use to split the tree.

1.2 Tree Splitting Algorithm

We use greedy method for tree splitting: start from the root tree, we traverse all the features and values and find out the feature value which has the maximum gain.

1.2.1 Exact Greedy Algorithm

Basically we sort each feature and linearly scan all the features and values

1.2.2 Approximate Algorithm

We can see that the last algorithm is quite time consuming so the author wants to come up with an approximation algorithm for speeding up. The algorithm first proposes candidate splitting points according to percentiles of feature distribution. The algorithm then maps the continuous features into buckets split by these candidate points, aggregates the statistics and finds the best solution among proposals based on the aggregated statistics.

2. Others

There are several more innovations related to XGBoost which I will talk in this part

2.1 Sparsity-aware Split Finding

XGBoost introduces default direction to deal with the sparse or missing values. What it does is to let the model itself to learn the optimal default directions from data.

Specifically, for every split the system will calculate the Splitting Gain for both putting all the sparse value in the left tree and right tree. Then choose the direction which has larger gains.

2.2 System Design

One of the great innovation of XGBoost is it uses parallel learning and cache-aware access to speed up the calculation.

3. Parameter Explanation

Finally, let's look at how we can leverage XGBoost in Python:
Jupyter Notebook For XGBoost Implementation

We can visualize the tree structure to get the insights as well as find the feature importance for further selection:

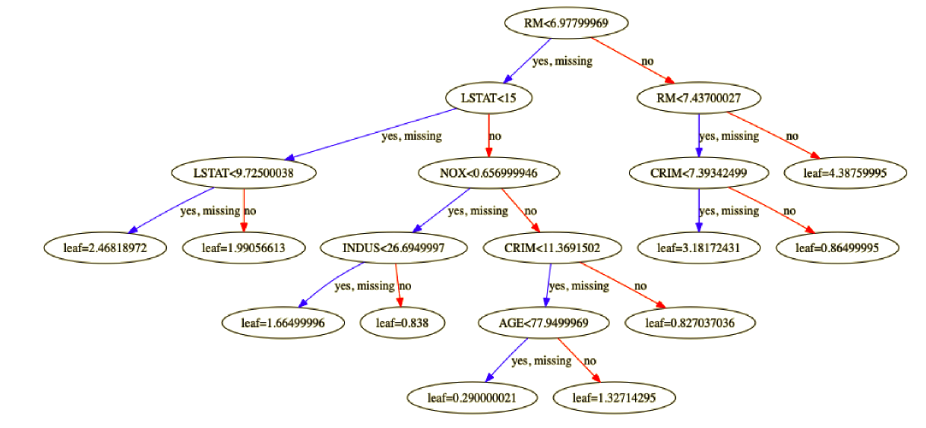
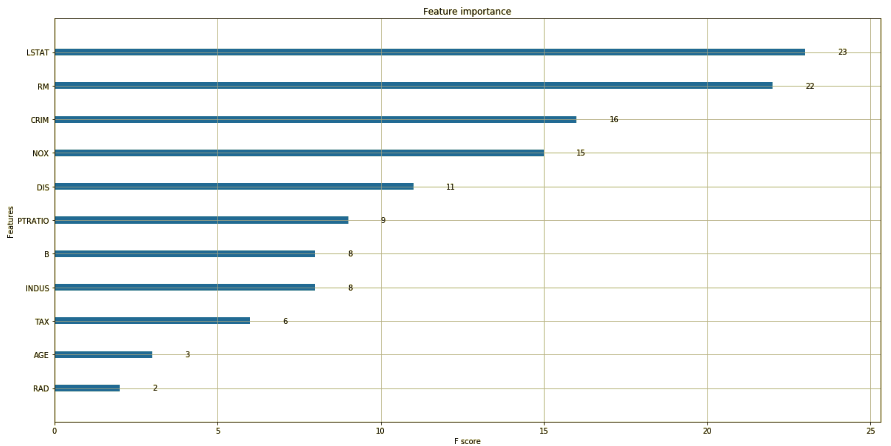
Reference:
https://arxiv.org/abs/1603.02754
https://www.datacamp.com/community/tutorials/xgboost-in-python
https://blog.csdn.net/wzmsltw/article/details/50994481
https://xgboost.readthedocs.io/en/latest/python/python_api.html