Inference Review (Part1)

Deep dive into statistics

Posted by Fan Gong on January 6, 2018

Last time we review the basic knowledge of Probability Theory, which gives us a fundamental understanding about statistics. This time we will go to the next step -- statistical inference.

Inference aims to learn about unknown quantities after observing some data that we believe contains relevant information. Normally, a statistical model specifies a joint distribution for observable random; parameters of that distribution are assumed unknown.

  • When we treat unknown parameters as fixed => "Frequentist" approach to statistical inference.
  • When we treat unknown parameters as random => "Bayesian" framework

    • 1. Parameter Estimation

    1.1 Point Estimation

    MLE (Maxmize Likelihood Estimation)
    We want to find the MLE of $\theta$, $\hat{\theta}=g(x_1,...,x_n) s.t. L(\hat{\theta}) \ge L(\theta) $ for all other $\theta$.
    The intuition here is that suppose we know the distribution of the sample data, we want to find the parameter that maximize the likelihood that we get these sample data.
    MME (Method of Moments)
    Compute moments such as $$E(X_i)=\mu, \quad E(X_i-\mu)^k$$, then equate sample moments to theoretical moments $$ \bar{X_n}=\mu, \quad \frac{1}{n}\sum(X_i-\bar{X})^k=E(X_i-\mu)^k $$ Bayes Estimator:
    Let $L(\theta,\hat{\theta})$ be a loss function. $E_\pi(L(\theta,\hat{\theta}))$ is the bayes risk. An estimator $\hat{\theta} $is said to be a Bayes estimator if it minimizes the Bayes risk among all estimators.
    Some notes on Bayes framework:
    $$f(\theta|x_1,...,x_n) = \frac{f(x_1,...,x_n|\theta)h(\theta)}{f_x(x_1,...,x_n)}$$

  • $h(\theta)$ - prior distribution of $\Theta$. Which is that prior belief about $\Theta$, here we choose based on experience.
  • $f(x_1,...,x_n|\theta)$ - Our model of data given a specific value of $\Theta=\theta$. Or we could say, the likelihood we observe these data based on this distribution.
  • $f_x(x_1,...,x_n)$ is the marginal distribution of x. So we will get a constant if we assign x equals to $x_1,...,x_n$.
  • $f(\theta|x_1,...,x_n)$ - posterior distribution. We collect data $x_1,...,x_n$ from experiment and update our beliefs about $\Theta$.

    • 1.2 Interval Estimation

    Some Important Distribution

    • Chi-square distribution:

      • Is a special gamma distribution when a = n/2 and b = 2; In particular, $$x_1,...x_n \sim ^{iid} N(0,1); then \sum_{i=1}^{n}x_i^{2}\sim x^{2}(n) $$
    • t-distribution:

      • If $W\sim N(0,1)$ and $V\sim X^2(r)$ and $W\perp V$, then $$T=\frac{W}{\sqrt{V/r}}\sim t(r)$$
    • F-distribution

      • If $U\sim X^{2}(r_1)$, $V\sim X^2(r_2)$, and $U\perp V$, then $$F = \frac{U/r_1}{V/r_2}\sim F(r_1,r_2)$$
    Very Useful Application
    If $\bar{X} \sim N(\mu, \sigma^2/n)$, $\bar{X}\perp S^2$, then we have: $$\frac{(n-1)S^2}{\sigma^2}\sim X^2(n-1)$$ Based on the above two distributions, we could get: $$\frac{\bar{X}-\mu}{S}\sqrt{n} \sim t(n-1)$$ Quantiles of distribution
    For any distribution, let $\alpha^{th}$ quantile (upper percentage point) be $$F(X_{\alpha})=P(X\le X_{\alpha}) = 1-\alpha$$ Confidence Interval
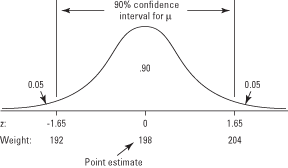
    In statistics, a confidence interval (CI) is a type of interval estimate that is computed from the observed data. The confidence level is the frequency of possible confidence intervals that contain the true value of their corresponding parameter. The intuiation here is that we try to find a function $u(X, \theta)$ such that its distribution does not depend on $\theta$. Then we look for a,b s.t. $$P(a< U(X, \theta)< b)=1-\alpha$$ and finally invert this to get a statement about $\theta$ $$P(f_1(x;a,b))<\theta< P(f_2(x;a,b))$$

    1.3 Important Interval Estimation Summary

    1.3.1 Sample Mean

    Let $X_1,...,X_n \sim N(\mu, \sigma^2)$

    • $\sigma$ is Known:
      • $$\frac{\bar{X}-\mu}{\sigma}\sqrt{n}\sim N(0,1)$$
    • $\sigma$ is Unknown:
      • $$\frac{\bar{X}-\mu}{S}\sqrt{n}\sim t(n-1)$$

    1.3.2 Sample Proportion

    Let $X_1,..., X_n \sim Bernoulli(P)$, n kown, $Y = \sum X_i \sim Bin(n, p)$. We will use an approximation to construct a CI for p. Recall, by central-limit theorem: $$\frac{Y-np}{\sqrt{np(1-p)}}\sim N(0,1)$$then we have $$\frac{Y}{n}-Z_{\alpha/2} \sqrt{\frac{P(1-P)}{n}} < P<\frac{Y}{n}+Z_{\alpha/2} \sqrt{\frac{P(1-P)}{n}}$$ Here we need to use MLE to get the point estimation of $\hat{P}= \frac{Y}{n}$

    1.3.3 Sample Variance

    Let $X_1,...,X_n \sim N(\mu, \sigma^2)$, both $\mu$ and $\sigma$ are unknown. $$\frac{(n-1)S^2}{\sigma^2} \sim X^2(n-1)$$ Brief Summary: For sample mean and proportion, if our sample size is large or we know the $\mu$ and $\sigma$, we normally use z-statistics; If we do not know $\sigma$, we will use t-statistics. For sample variance, we use chi-square statistics.

    Interval Estimation

    2. Hypothesis Testing

    Here is a basic set up for a hypothesis test: we have some default belief about a parameter, this is our null hypothesis. And we're trying to investigate whether an alternative hypothesis is in fact true.

    2.1 Some definations and summary

    Type I and II error
    Upon conducting a test we will arrive at one of two possible conclusions:

  • Reject $H_0$: sufficient evidence against $H_0$
  • Not Reject $H_0$: Not enough evidence
    • Then it is reasonable that we will make errors.
    $H_0$ is True $H_A$ is True
    Reject $H_0$ Type I error Correct
    Not Reject $H_0$ Correct Type II error

    More specifically, Type I Error equals to $P(\theta \in C|H_0)$, which means when $H_0$ is true, the probability that our parameter locates in critical region (rejection region). Type II Error equals to $P(\theta \in C^c|H_A)$, which means when $H_A$ is true, the probability that our parameter locates in the non-rejection area.

    Based on the analysis above, we could see an obvious trade-off between these two type of errors. Since if we shrink the rejection area to decrease type I error, the non-rejection area will be larger which means the type II error will increase. The reason that we always first control type I error is that:

    In practical, our null hypothesis is always very specific, whereas the alternative hypothesis is always very general. For example, $H_0=1000$, then $H_A\ne 1000$. Therefore, in comparison, we are more willing to know the error that one specific hypothesis is actually false.
    Significance Level

    In practice, we often specify the maximal allowable type I error. Specifically, $P(\theta \in C|H_0) \le \alpha$, where $\alpha$ is the significance level. In another word, it defines the probability of rejecting the null hypothesis when it is true.

    P value
    P value is the probability of observing a result equal to or more extreme than what was actually observed, when $H_0$ is true.

    Intuition Here: We start by saying assume $H_0$ is true. We collect data, and analyze it in some manner. When we look at that summary, the p-value let us know how reasonable our data is, assuming the null is true. When the p-value is small, it tells us one of two things. 1) If the null hypothesis is true, then we’re seeing something that’s unlikely or 2) these data are really incompatible with the null hypothesis (because we had a low chance to see this or more extreme results), therefore, I suspect the null hypothesis does not hold. Your job is to pick an alpha level to decide your comfort in making a Type I error.

    Example:
    We want to construct a hypothesis test about whether this person is guilty or not. Suppose he is innocent, after observing some data, we find the probability that these resources appear is 4%. And our significance level is 0.05. Based on that, we could reject our null hypothesis.



    In a word, we could see that the key idea behind Hypothesis Testing is that we think small probability event is not gonna happen easily. We will set a threshold (significnace level) to define the tolerance level for this small probability event; and p value will tell us the probability of obtaining at least as extreme as the one in our sample data, assuming the truth of the null hypothesis. After compare this p value with our significace value, we can then make a decision to accept or reject our hypothesis.

    2.2 Constructing Hypothesis Tests

    After understanding the whole process of hypothesis testing, we will then wonder how to choose the best critical region. Since it is the most important part of our test. In general, the best critical region of size $\alpha$ is that for every subset $A$ such that $P_{H_0}(x \in C) = \alpha$, we have $P_{H_A}(x \in C^c) \le P_{H_A}(x \in A^c)$. Which means we have minimum type II error with fixed type I error.

    We have three method to find the best critical region:

  • Neyman-Pearson Lemma (simple to simple)
    • Suppose we have a random sample $X_1, X_2, ..., X_n$ from a probability distribution with parameter $\theta$. Then, if $C$ is a critical region of size $\alpha$ and $k$ is a constant such that: $$\frac{L(\theta_0)}{L(\theta_α)}≤k$$ inside the critical region C and: $$\frac{L(\theta_0)}{L(\theta_α)}\ge k$$ outside the critical region C then $C$ is the best, that is, most powerful, critical region for testing the simple null hypothesis H0: $θ = θ_0$ against the simple alternative hypothesis HA: $θ = θ_a$.

  • Uniformly Most Powerful Tests (simple to composite)
    • Basically, UMP is an extension of NP lemma. We could select one from the composite set, and test $H_0$ against each one in $H_A$.

  • Likelihood Ratio Tests (composite to composite)
    • May not get the best critical regions, but reasonable and have desired properties. The LRT use test statistics $$\Lambda = \frac{max_{\theta\in H_0}L(\theta)}{max_{\theta\in \Omega}L(\theta)}$$ to reject $H_0$ for small values of $\Lambda$.

    Let us talk about other inference knowledge in the next post!